A-时间表查询！

\hspace{15pt} 今天是2025年1月25日，今年的六场牛客寒假算法基础集训营中，前两场比赛已经依次于 20250121、20250123 举行；而后四场比赛将依次于 20250126、20250206、20250208、20250211 举行。
\hspace{15pt} 小歪想知道第 $x$ 场比赛是否已经举行，你能帮帮他吗？

解题思路

直接输出。

参考代码

#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 2e5 + 10;

void solve(){
	int n;
	cin >> n;
	if(n <= 2){
		cout << "YES\n";
	}else{
		cout << "NO\n";
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int t = 1;
//	cin >> t;
	
	while(t --){
		solve();
	}
}

B-一起做很甜的梦！

\hspace{15pt} 梦境是由我们的记忆碎片重组后再次演绎的结果。对于一个拥有 $n$ 段记忆的人，我们可以使用 $1\sim n$ 这 $n$ 个整数来表示每一段记忆。将这 $n$ 段记忆打乱后重新组合，就得到了一个梦。
\hspace{15pt} 作为牛客星球的首席梦境研究员，牛可乐在研究中发现：如果一个梦境中任意连续的 $k$ 段记忆（其中 $1<k<n$）都无法完整还原出一段真实经历时（即不构成一个排列），这个梦就会特别甜美。这种恰到好处的记忆重组方式，让梦境与现实保持着微妙的距离，创造出令人陶醉的朦胧美感。
\hspace{15pt} 现在，牛可乐想请你帮忙设计一些这样的甜美梦境，来继续他的天才研究。

\hspace{15pt} 长度为 $n$ 的排列是由 $1\sim n$ 这 $n$ 个整数、按任意顺序组成的数组，其中每个整数恰好出现一次。例如， { 2 , 3 , 1 , 5 , 4 } \{2,3,1,5,4\} {2,3,1,5,4} 是一个长度为 $5$ 的排列，而 { 1 , 2 , 2 } \{1,2,2\} {1,2,2} 和 { 1 , 3 , 4 } \{1,3,4\} {1,3,4} 都不是排列，因为前者存在重复元素，后者包含了超出范围的数。

解题思路

要求任意连续的子区间都不能构成排列，奇数从小到大偶数从大到小输出即可。

参考代码

#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 2e5 + 10;

void solve(){
	int n;
	cin >> n;
	vector<int> ans1,ans2;
	for(int i = 1;i <= n;i ++){
		if(i & 1){
			ans1.push_back(i);
		}else{
			ans2.push_back(i);
		}
	}
	for(auto x : ans1){
		cout << x << " ";
	}
	sort(ans2.begin(),ans2.end(),greater<int>());
	for(auto x : ans2){
		cout << x << " ";
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int t = 1;
//	cin >> t;
	
	while(t --){
		solve();
	}
}

C-翻之

\hspace{15pt} 对于给定的 $n$ 行 $m$ 列的矩阵，每一个元素要么是 $\text{‘0’}$，要么是 $\text{‘1’}$。
\hspace{15pt} 每一轮，你可以进行一次以下操作：
$\bullet$选择一行的元素，将其全部反置，即 $\text{‘0’}$ 变为 $\text{‘1’}$，$\text{‘1’}$ 变为 $\text{‘0’}$。
\hspace{15pt} 请你帮助小歪判断，若能进行任意多轮操作（也可以不进行操作），至多能使得多少列的元素均为 $\text{‘1’}$。你只需要输出这个最大值。

解题思路

每次操作将一行的元素都会进行反置，那么其实对于每一列的元素都会有影响。
所以两列如果能够同时为全1列的话，那么必然这两列初始状态就是相同的。
比如下面的一个矩阵：

0 0 1 1 1
1 0 0 0 0
1 0 1 1 1
1 0 1 1 0

取第三列为：1 0 1 1
取第五列为：1 0 1 0
无论如何进行操作都无法将第三列和第五列都变为1 1 1 1。
因为每次操作是将两列同一位置的元素进行反置，如果同一位置的两个元素不同的话无论如何反置都无法相同。只有相同才能变相同，不同必不相同。
所以答案就是取相同列的最大值。

参考代码

#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 2e5 + 10;
void solve(){
	int n,m;
	cin >> n >> m;
	vector<string> s(m + 1);
	for(int i = 1;i <= n;i ++){
		for(int j = 1;j <= m;j ++){
			char c;
			cin >> c;
			s[j] += c;
		}
	}
	map<string,int> mp;
	int ans = 1;
	for(int i = 1;i <= m;i ++){
		mp[s[i]] ++;
		ans = max(ans,mp[s[i]]);
	}
	cout << ans;
	

}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int t = 1;
//	cin >> t;
	
	while(t --){
		solve();
	}
}

D-乘之

\hspace{15pt} 对于给定的由 $n$ 个整数组成的数组 { a 1 , a 2 , … , a n } \{a_1,a_2,\dots,a_n\} {a1​,a2​,…,an​}，小龙和小蛇借助于此数组进行游戏。
\hspace{15pt} 游戏步骤如下：
${}_{\text{1.}}$小龙选择一个非空区间 $[a,b]$；
${}_{\text{2.}}$小蛇选择一个非空区间 $[c,d]$；
${}_{\text{3.}}$将选中的区间中的全部元素均乘上 $k$，得到数组 $a^{\prime }$；
\hspace{15pt} 游戏只进行一轮，三个步骤结束后立即停止。
\hspace{15pt} 小龙想要让数组 $a^{\prime }$ 的元素之和尽可能大，小蛇想要让数组 $a^{\prime }$ 的元素之和尽可能小。假设双方都采取的是最优策略，请你计算操作后得到的数组 $a^{\prime }$ 的元素之和。

\hspace{15pt} 请注意，区间 $[a,b]$ 和 $[c,d]$ 可以相交，但只结算一次，即若某一个位置被小龙和小蛇同时选中，依旧只乘一次。

解题思路

一开始用的区间最大值、最小值去做的这题，但是好像可以通过最优策略得出结论。
先说结论：整个数组乘以k就是答案。
听起来是不是有点神秘，但其实通过最优策略确实是这么个道理。
首先第一个人选取的区间肯定是最利于他自己的，那么剩下的区间（可能是0个、1个、2个）就是不利于第一个人的，但是一定是利于第二个人的。并且题目说了两个人取得区间交集不会重复计算，那么无论在第一个人取了区间后剩下多少个区间，第二个人都可以把剩下的区间当作一个区间来取走。
所以在两个人的最优策略下整个数组的元素会刚好被使用一次。

参考代码

#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 2e5 + 10;

void solve(){
	int n,k;
	cin >> n >> k;
	vector<i64> a(n + 1);
	for(int i = 1;i <= n;i ++){
		cin >> a[i];
	}
	i64 ans = 0;
	for(int i = 1;i <= n;i ++){
		ans += a[i] * k;
	}
	cout << ans << "\n";
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int t = 1;
	cin >> t; 
	
	while(t --){
		solve();
	}
}

E-在树上游玩

\hspace{15pt} 对于给定的由 $n$ 个节点组成的无根树，每一条边都可以被染上颜色，初始时，全部边均为白色。
\hspace{15pt} 现在，选中树上 $k$ 个不同的点，并将它们标记，随后，定义，如果一条树边 $(u,v)$ 满足节点 $u$ 和 $v$ 同时被标记，那么这条树边自动被染为红色，不需要花费任何代价。

\hspace{15pt} 现在，你可以额外选择一些树边，将它们染成红色，每染一条边需要花费 $1$ 点代价。
\hspace{15pt} 请你计算最小的染色代价，使得任意一个被标记的点都可以通过被染成红色的边到达至少一个未被标记的点。并输出不同的染色方案数量。

解题思路

用dsu计算红边相连的连通块有几个，然后每个连通块的最近子节点的个数相乘就是ans。

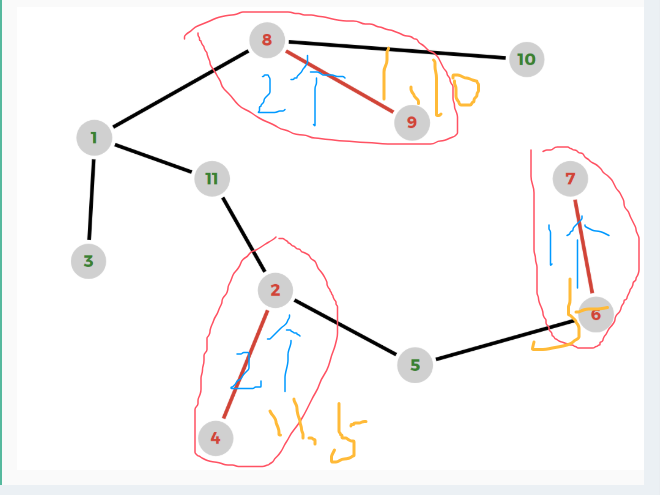
每个红圈代表一个连通块，蓝色的字表示有几个最近子节点，黄色的是哪几个最近子节点。

参考代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
using i64 = long long;
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
void solve(){
	int n,k;
	cin >> n >> k;
	vector<int> sig(n + 1);
	for(int i = 1;i <= k;i ++){
		int x;
		cin >> x;
		sig[x] = 1;
	}
	vector<vector<int>> g(n + 1);
	vector<int> fa(n + 1),cnt(n + 1);
	for(int i = 1;i <= n;i ++){
		fa[i] = i;
		cnt[i] = 0;
	}
	auto find = [&](auto &&find,int x)-> int{
		if(fa[x] != x){
			return fa[x] = find(find,fa[x]);
		}
		return fa[x];
	};
	for(int i = 1;i < n;i ++){
		int u,v;
		cin >> u >> v;
		if(sig[u] && !sig[v]){
			cnt[find(find,u)] ++;
		}
		if(sig[v] && !sig[u]){
			cnt[find(find,v)] ++;
		}
		
		if(sig[u] && sig[v]){
			int fa1 = find(find,u);
			int fa2 = find(find,v);
			if(fa1 == fa2){
				continue;
			}
			cnt[fa1] += cnt[fa2];
			fa[fa2] = fa1;
		}
	}
	int ans1 = 0,ans2 = 1;
	for(int i = 1;i <= n;i ++){
		if(sig[i] && fa[i] == i){
			ans1 ++;
			ans2 = ans2 * cnt[i] % mod;
		}
	}
	cout << ans1 << " " << ans2 << "\n";
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int t = 1;
//	cin >> t;
	
	while(t --){
		solve();
	}
}